A couple of months ago, I posted an approximate formula for the longest match in the problem of DNA alignment. I recently used it to calibrate a seeding heuristic to map Illumina reads and I was surprised to see that it was not just bad, but epic bad. Upon closer inspection, I realized that the main assumption does not hold when the error rate is small (which is typically the case for Illumina reads). The formula was based on longest runs in Bernoulli trials. This time I present more accurate results with an approach based on a stick breaking process.

Stick breaking (spacings)

Inserting $(k)$ mutations at random in a sequencing read will produce $(k+1)$ (possibly empty) subsequences without errors. The process is analogous to inserting $(k)$ breaks at random in a stick of length 1, and we can approximate the distribution of the longest subsequence without error by that of the longest fragment when breaking the stick.

The example above illustrates this concept graphically. A sequencing read of 60 nucleotides contains 2 mutations highlighted in red and the longest error-free stretch is the central subsequence of 28 nucleotides. If mutations occur uniformly on the read, the longest error-free subsequence can be modelled by the longest fragment when inserting two breaks in the stick (colored in red).

The fragments of a broken stick are known as “uniform spacings” and their distribution is known for a long time. For such a long time that it is almost forgotten (as in “there is no Wikipedia page on spacings ”). To get the full picture, I had to ask the community on CrossValidated, where I also posted the proofs of the main results after I got some help. The distribution is relatively simple and is asymptotically Gumbel (but the approximation is good only for $(k \geq 50)$ breaks, which is irrelevant in this context). Since we will need it later, the cumulative distribution of the longest fragment when inserting $(k)$ breaks is

$$P(Z_k \leq x) = \sum_{j=0}^{k+1} {k+1 \choose j} (-1)^j (1-jx)_+^k,$$

where $(a_+ = a)$ if $(a >0)$ and $(0)$ otherwise.

Longest error-free stretch

The result above assumes that the stick has length 1 and that the number of breaks $(k)$ is fixed and known. In practice, a read has variable length and we do not know the number of errors. We need to adjust the formula for a stick of length $(m)$ (counted in nucleotides) and to integrate for all possible values of $(k)$. For a fixed error rate equal to $(q = 1-p)$, the number of mutations has a binomial distribution. Denoting the size of the longest error-free stretch from a read of length $(m)$ as $(X_m)$, the cumulative distribution comes as

$$ P(X_m \leq x) = \sum_{k=0}^{m} {m \choose k} q^kp^{m-k} P \left(Z_k \leq \frac{x}{m-k} \right). $$

Finally, the probability that a read of length $(m)$ contains at least one error-free stretch of size at least $(x)$ is $(P(X_m \geq x) = 1 - P(X_m \leq x))$. The only approximation in this formula is that the length of error-free stretches is discrete and not continuous.

Below is a representation of this probability for an instrument with a 2% error rate. I have plotted the probability that a read of the given size contains at least one seed (perfect match with the reference) of the given length. The curve for reads of 50 bp stops with a dot to highlight that beyond that point, the probability is 0.

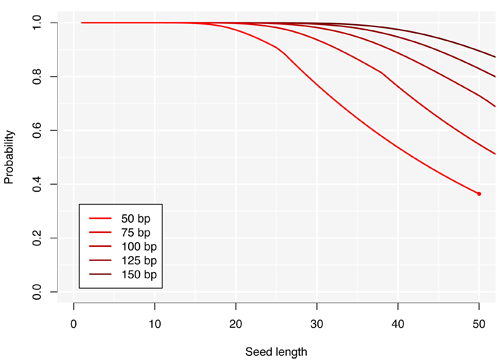
The kinks in the curves for reads of 50 and 75 bp are not graphical artefacts, they are really there in the distribution. The graph suggests that seeds of length 17 are good as long as we can sequence 50 nucleotides in a row with this machine, because 99% of the reads will have an error-free stretch of 17 bp of longer. This is nice because 17-mers have on average less than 1 occurrence in the human genome, so we will have to perform few alignments to validate the hits.

Good strategies sometimes allow a few mismatches in the seed (typically 1). Unfortunately, the distribution of the longest consecutive fragments in the stick breaking approach presented above is harder to derive, so this result is essentially useful for error-free seeding strategies.

# Set the error rate to 2%.
q = 0.02
p = 1-q 

# Convenience function to return the positive part.
pos = function(x) (abs(-x)+x) / 2 

# Cumulative probability of the longest fragment of a unit stick
# with k breaks.
PZ = function(k,x) {
   if (x >= 1) return (1) 
   j = 0:(k+1)
   sum(choose(k+1,j)*(-1)^j*pos(1-j*x)^k)
}

# Cumlative probability of the longest fragment of a stick of length
# m with Binomial errors.
PX = function(m,x) {
   v = 0 
   for (k in 0:m) {
      v = v + dbinom(prob=q, size=m, k) * PZ(k, x/(m-k))
   }   
   v   
}

X150 = c(1, 1 - sapply(1:74, PX, m=150))
X125 = c(1, 1 - sapply(1:74, PX, m=125))
X100 = c(1, 1 - sapply(1:74, PX, m=100))
X75 = c(1, 1 - sapply(1:74, PX, m=75))
X50 = c(1, 1 - sapply(1:49, PX, m=50))

COL = colorRampPalette(c("red", "black"))(8)

pdf("seedlength2.pdf", height=6, width=7.5)

plot(X50, type='n', xlab="Seed length", ylab="Probability",
   ylim=c(0,1), xlim=c(0,50), bty="n")

rect(xleft=-10, xright=60, ybottom=-.5, ytop=1.5, col="grey96", border=NA)
abline(v=seq(0,50,by=10), lwd=2, col="white")
abline(v=seq(5,45,by=10), lwd=1, col="white")
abline(h=seq(0,1,by=.2), lwd=2, col="white")
abline(h=seq(.1,.9,by=.2), lwd=1, col="white")

lines(X150, lwd=2, col=COL[5])
lines(X125, lwd=2, col=COL[4])
lines(X100, lwd=2, col=COL[3])
lines(X75, lwd=2, col=COL[2])
lines(X50, lwd=2, col=COL[1])
points(50, X50[50], pch=19, col=COL[1], cex=.6)

legend(legend=c("50 bp", "75 bp", "100 bp", "125 bp", "150 bp"),
   x="bottomleft", bg="white", inset=0.05, col=COL[1:5], lwd=2)

dev.off()