The first thing you learn in statistics is that “correlation does not imply causation”. As obvious as it sounds, most human mistakes fall in this category, and not only in statistics. The major difficulty with this question is that it is fairly easy to define correlation, but it is much harder to define causation, let alone quantify it. No surprise many statisticians just avoid talking about causation to stay out of the danger zone.

However, for Judea Pearl, this is not a satisfactory answer. In his book Causality: Models, Reasoning, and Inference, he expresses his opinion vividly.

I see no greater impediment to scientific progress than the prevailing practice of focusing all our mathematical resources on probabilistic and statistical inferences while leaving causal considerations to the mercy of intuition and good judgment.

This book lays the foundation of the now popular Bayesian networks. The key idea is that you can distinguish correlation from causation if you can observe several independent causes. For instance, suppose that patients suffering from a certain type of cancer are often immunodeficient. You wonder whether immunodeficiency is a cause or a consequence of this cancer type.

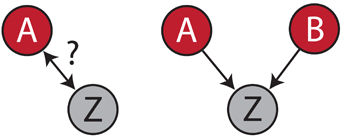
Say that variable A is whether patients have cancer and Z is whether they are immunodeficient. If all you know is that A and Z tend to co-occur, you cannot decide anything. One or the other may be the cause, or they could both be due to something else. But if you also observe a variable B, say a fungal infection, you may hit the jackpot. If A and B are not correlated, but they are each correlated to Z, then Bayesian networks tell you that A and B are causes of Z. Here is why: if cancer and fungal infections were a consequence of immunodeficiency, they should occur on the same individuals, so they should be correlated. This would also be the case if only one of those were the consequence of the immunodeficiency. So the only case that is left is that immunodeficiency is a consequence of either cancer or fungal infection.

Of course, there is a lot more theory and mathematics behind it, but this is in a nutshell the principle of Bayesian networks. It is important to understand that this kind of inference is only possible when A and B are each correlated with Z but not correlated with each other. In the other cases, we still cannot say much (note that the formal criterion is more complex and involves the conditional distribution of A and B given Z).

It is often claimed that the edges of Bayesian networks represent causal relationships, but Judea Pearl specifically defines “causal” Bayesian networks, which means that they do not all have this property. There are three conditions for a Bayesian network to be causal, and even though they are quite technical, they seem fairly reasonable at first sight.

However, here is what can happen if there are unobserved variables. Imagine that infection by a virus causes both immunodeficiency and the cancer type mentioned above. Also imagine that we are completely unaware of this fact. If C is the infection by the virus, the real flow of causes-consequences would be as shown below.

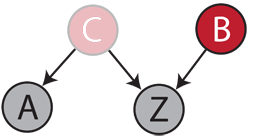
If B and C are uncorrelated, then A and C are also uncorrelated, and if C causes both A and Z, then A and Z are correlated. So this case is indistinguishable from the previous one. Causal Bayesian network inference would conclude that A is a cause of Z, predicting that if you treat the cancer, the immune system of the patients will recover. That would be a mistake.

So what is the problem with causal Bayesian networks if the assumptions do not seem unreasonable? The problem is not whether they are reasonable, but that they cannot be checked without experimental testing. Put loosely, the third condition for causal Bayesian network inference to be valid is that forcing a variable to have a certain value (for instance treating the cancer) is the same as observing that value (observing a patient without cancer). More specifically, the conditional distributions must be identical in both cases. The only way to verify this is to actually do the experiment, which as a side effect will also answer your initial question.

According to George Box’s famous comment “all models are wrong, but some are useful”. I have no doubt that Bayesian networks can be useful. However, in natural sciences interpreting edges as causal relationships is impossible because of unobserved variables. So far, the only way to be sure is experimentation, and there is no other serious contender to understand cause-consequence relationships.