The problem of sequence alignment gets a lot of attention from bioinformaticians (the list of alignment software counts more than 200 entries). Yet, the statistical aspect of the problem is often neglected. In the post Once upon a BLAST, David Lipman explained that the breakthrough of BLAST was not a new algorithm, but the careful calibration of a heuristic by a sound statistical framework.

Inspired by this idea, I wanted to work out the probability of identifying best hits in the problem of long read alignments. Since this is a fairly general result and that it may be useful for many similar applications, I post it here for reference.

Longest runs of 1s

I start with generalities on series of 0s and 1s and focus on the distribution of the longest run of 1s. This general problem has many applications, and I will explain why it is important for sequence alignment in the next section.

Assume that we have a Bernoulli sequence of length $(n)$ such that the probability of a 1 is $(p)$ and the probability of a 0 is $(1-p = q)$. Let $(X_0)$ be the longest run of 1s in the series. As $(n)$ increases, the number of 0s in the series tends to $(nq)$, so the number of runs of 1s also tends to $(nq)$ (allowing runs of length 0). As a result, the longest run of 1s is approximately distributed as the maximum of $(nq)$ geometric variables with parameter $(p)$. Assuming that $(m = nq)$ is an integer and denoting each geometric variable by $(Y_i)$, we obtain

$$ P(X_0 \leq x) \approx \prod_{i=1}^m P(Y_i \leq x) = \prod_{i=1}^m \left(q + pq + \ldots + p^xq \right) = (1-p^{x+1})^m. $$

Now using $(nq)$ instead of $(m)$ and approximating the logarithm the usual way, we get

$$ P(X_0 \leq x) \approx \exp \left(qn \ln(1-p^{x+1}) \right) \approx \exp \left(-nq p^{x+1} \right) . $$

The asymptotic mean of $(X_0)$ is $(\log_{1/p}(qn) +\gamma/\ln(1/p) - 1/2)$, where the Euler constant $(\gamma \approx 0.5772)$. As an example, we can use these formulas for tosses of a fair coin. The average length of the longest run of Heads in 200 tosses of a fair coin is close to 7, and around 1/3 of the sequences will contain a run of Heads longer than 7.

We are also interested in $(X_k)$, the longest run of 1s interrupted by $(k)$ 0s. Since the mathematics is more challenging, I will state the result without explanation. The interested readers can obtain the detail from reference [1].

$$ P (X_k \leq x) \approx \exp\left( -\frac{a^k}{k!} nqp^{x+1} \right), \text{where } a = \frac{q\ln(n)}{p\ln(1/p)}.$$

Note that the first formula is the special case of the second for $(k = 0)$. Even though the parametrization I chose does not make it explicit, the limit distribution is a Gumbel, also known as the double exponential or extreme value distribution.

Application to seed methods

Many sequence alignment algorithms use a seed method to quickly eliminate large parts of the search space. Seeds are perfect (or near perfect) matches between sequences, which are used to “anchor” the alignment. This saves time because it is less computationally expensive to search perfect matches than to perform exact sequence alignment by dynamic programming methods. Since there is no guarantee that the best hit contains a seed, it is important to control the false negative rate.

To give a concrete example, let us say that we want to align a 100 bp PacBio read with 15% error rate (and no autocorrelation). PacBio reads are usually longer, but the sequences could be intrinsically shorter, like exons and restriction fragments for instance. If the 100 bp sequence is present in the genome, the alignment will have about 85 matches and 15 non matches, and it will be seeded if it contains enough consecutive matches. By encoding a match as a 1 and a non match as a 0, we can use the results of the previous section to know the probability that the alignment contains a seed of a certain length. For this, we have to study the longest run of 1s in a Bernoulli series of length 100 where the probability of a 1 is $(p = 0.85)$.

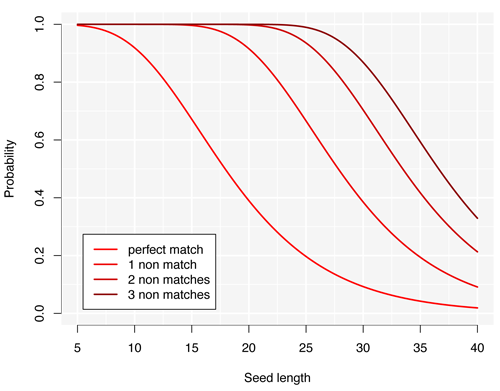
The figure above summarizes the probabilities that the alignment contains a seed of a given length for different degrees of tolerance representing the number of non matches allowed in the seed. The graph illustrates several important features of this alignment problem.

1. Perfect seeds are inefficient. Seeds as short as 10 nucleotides already incur a 10% chance of missing the hit. Yet for a reference of the size of the human genome, there will be thousands of spurious seeds. As a result, the search will lack both speed and sensitivity.
2. Non matches show diminishing returns. The curves are increasingly closer to each other as the number of allowed non matches increases. This means that allowing one non match has the best “relative improvement”. For instance, more than 30% of the hits are missed by using perfect seeds of 15 nucleotides, which goes down to 1% by allowing one non match.
3. Two may still be better than one. To keep the false negative rate at 1%, seeds allowing 2 non matches have to be 22 nucleotides or shorter. A back of the envelope calculation shows that the number of spurious seeds in the human genome is around 5, whereas it is 100 times as much for seeds of length 15 allowing 1 non match. It then depends on which takes longer: finding all seeds with 2 non matches or doing all the alignments. Here the answer depends on the strategy.

It is important to insist that these conclusions are valid only in the context of the example I chose. For longer reads, perfectly matching seeds may be well adapted. The point is that those formulas are very handy to calibrate alignment methods in non standard applications, or when hits can be intrinsically short (the most obvious case being the de novo identification of exons).

n = 100
p = .85
q = .15
x = seq(5, 40, by=.1)
plot(x, 1-exp(-((q/p*log(n)/log(1/p))^2)/2 * n*q*p^(x+1)), ylim=c(0,1),
   type="n", ylab="Probability", xlab="Seed length", bty="n")
rect(xleft=0, xright=50, ybottom=-1, ytop=2, col="grey96")
abline(v=seq(5,40, by=5), col="white", lwd=2)
abline(h=seq(0,1, by=.2), col="white", lwd=2)
abline(v=seq(7.5,42.5, by=5), col="white", lwd=1)
abline(h=seq(0.1,.9, by=.2), col="white", lwd=1)
lines(x, 1-exp(-(n*q*p^(x+1))), lwd=2, col="red1")
lines(x, 1-exp(-(q/p*log(n)/log(1/p)) * n*q*p^(x+1)), lwd=2, col="red2")
lines(x, 1-exp(-((q/p*log(n)/log(1/p))^2)/2 * n*q*p^(x+1)), lwd=2, col="red3")
lines(x, 1-exp(-((q/p*log(n)/log(1/p))^3)/6 * n*q*p^(x+1)), lwd=2, col="red4")
legend(x="bottomleft", inset=.05, bg="white", lwd=2,
   col=c("red1", "red2", "red3", "red4"),
   legend=c("perfect match", "1 non match", "2 non matches", "3 non matches"))

References

[1] An extreme value theory for long head runs. Probability Theory and Related Fields. 1986;72(2):279-87.
[2] The Longest Run of Heads. The College Mathematics Journal, 1990;21(3):196-207.