Here is a discussion that I recently had with my colleague John. He approached me with the following request:

The danger of John’s approach

John claimed that there is no bias when first looking at the data, and then doing a one-tailed test. This is incorrect. To see this, I have generated random Gaussian data sets on which I have performed a one-tailed t test. As John suggests, I have changed the side of the tail depending on whether the first or the second sample had the greatest mean. I then recorded how many tests had a p-value lower than 0.05. Here is what it looks like for different sample sizes.

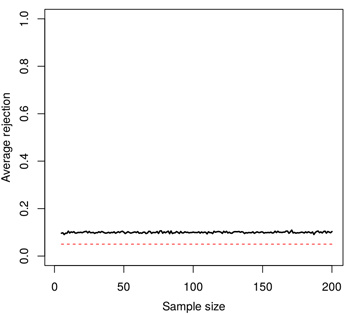
I have highlighted the 0.05 threshold by a red dotted line. The rejection rate of this procedure lies nicely above the horizontal line for all sample sizes. The theoretical value of the black line is 0.10, can you see why?

When performing a t test on random data (i.e. when the null hypothesis is true), the t statistic will be positive or negative with probability 1/2. The procedure described above is equivalent to swapping the samples such that the t statistic is always positive. If we call $(Q_{95})$ the 95-th percentile of the t distribution, the value we are looking for is $(P(t > Q_{95} | t > 0))$. But this is simply

$$P(t > Q_{95} | t > 0) = \frac{P(t > Q_{95} \cap t > 0)}{P(t > 0)} = \frac{P(t > Q_{95})}{1/2} = 2P(t > Q_{95}).$$

In conclusion, this approach doubles the risk of rejecting the null hypothesis when it is true. More worrisome, a risk of 0.10 will be claimed to be 0.05.

If you would like to see the code to generate the simulation, click the Penrose triangle below.

# Define a modified one-tailed t-test that first looks at the data
# and then decides which alternative to use.
cheat_test <- function(x,y) {
   alt <- ifelse(mean(x) < mean(y), "less", "greater")
   t.test(x,y, alternative=alt)$p.value
}

# Create a vector to store the average rejection rate.
# We vary the sample size from 5 to 200 in this example.
av <- rep(NA, 200)
for (ssize in 5:200) {
   # We perform 1000 replications of the test (increase
   # if you want more accuracy).
   pvals <- replicate(1000, cheat_test(rnorm(ssize), rnorm(ssize)))
   av[ssize] <- mean(pvals < 0.05)
}

When to use one-tailed tests?

I can see at least three cases where one-tailed tests are appropriate. I am sure that some would disagree, or find the list incomplete. I simply hope that these examples will help you make your own judgement.

1. Asymmetric distributions

Some tests are intrinsically one-tailed. The $(\chi^2)$ test for instance has a positive distribution with a right tail. A large value means a departure from expectations, so the rejection region is put exclusively on the side of large values. This way, the null hypothesis is not rejected when the scores have expected values.

A famous counterexample is found in the reanalysis of Mendel’s results by Fisher. The key argument of Fisher was that the values of the $(\chi^2)$ statistics were too small and thus that the samples were too much as expected, which he found suspicious. This usage of the $(\chi^2)$ test is rather unconventional, but it is still one-tailed.

I find the fact that Nature journals ask to specify the number of tails in the $(\chi^2)$ test rather confusing. This may lead some readers to believe that a two-tailed $(\chi^2)$ test is also sound.

2. Composite null hypotheses

This is rather a hack than an argument based on theory. The vast majority of null hypotheses are “simple” in the sense that they are true for a single value of the parameter under study (typically when it is equal to 0). This is rather problematic because we would sometimes like to test whether the mean is non-negative instead of just zero. In practice, it makes sense to achieve this with a one-tailed test for the null hypothesis that the mean is zero.

3. We measure only one tail

Sometimes, it is too costly or impossible to measure some events at one of the ends of the distribution. For instance, imagine that a company is testing new hardware components supposed to be more resistant to failure. To do so, they run their prototypes for months until failure, in parallel with current hardware as a control. If the prototypes fail before the current hardware, there is no point wasting time and resources to see how much better the current hardware is. This tail will never be observed, so the company might as well set up a one-tailed test.

One might argue that many cases fall in this category because the main point is that one of the possible outcomes is simply not “interesting”. For instance, is it really worth to discover drugs that are less efficient than the placebo? Or fortune tellers performing significantly worse than random? Here it depends on the context, but either way, this decision should be taken before having a look at the data.