Important note: Please read the Erratum at the end of the post.

Tolstoy’s remorse

It is 1879. Leo Tolstoy, then rich and famous for War and Peace and Anna Karenina works on another kind of text. In A Confession he explains at length that he regrets writing those novels. The focus of his remorse and his anger towards himself is the heart of his talent, this innate sense of human nature. Tolstoy's pen had no equal when it came to paint the Russian society of the time, its characters and its culture. However, he explains that this attitude towards writing is wrong, because he has been telling without preaching, he has been describing without judging. He will even abandon the royalties of War and Peace and Anna Karenina, refusing to earn money from such immoral writings.

We were all then convinced that it was necessary for us to speak, write, and print as quickly as possible and as much as possible, and that it was all wanted for the good of humanity. And thousands of us, contradicting and abusing one another, all printed and wrote — teaching others. And without noticing that we knew nothing, and that to the simplest of life’s questions: What is good and what is evil?

When Tolstoy finally came out of this existential crisis, his work was profoundly transformed. His later books have a heavy moralistic tone and even the best pieces The Death of Ivan Ilyich and The Kreutzer Sonata did not meet the standards of his first two novels. Remorse had killed the artist in him. Yet Tolstoy had realized with a too perfect lucidity the hazards of writing. He simply could not live with the idea that his books would inspire evil among his readers.

Science and conscience

The fear of inspiring the wrong is also there in science, but the cliché of the researcher destroying his work so that it is not put to bad use is just that: a cliché. In reality most discoveries have a limited scope, and they can all be rediscovered by someone else. Does that mean that scientists have no conscience when it comes to their work?

It is certainly not true about complicated issues such as mental disorders or racism. Quite the opposite, it is not easy to distinguish when researchers expose the result of their work or express a personal, moral opinion — most likely because they don't know it themselves. In Is there a gene for alcoholism? I argued that many studies that claim to discover a gene for alcoholism or homosexuality are actually a personal statement about human nature, something unrelated to science really.

About racism, the black book of genetics has two entries worth mentioning. Two times at least, scientific arguments were opposed to racism, but these arguments turned out to be wrong. Or even worse: manipulated. In spite of the contempt that these words inspire, I must take the necessary precaution to emphasize that the people I will mention in this series are recognized scientists, and that their scientific contribution is outstanding. I hope I will succeed in making their mistakes an occasion to learn, rather than an occasion to blame them.

Lewontin’s fallacy

The first case, due to Richard Lewontin, was made two times famous: first by the publication of the original argument in a seminal paper of 1972 (The Apportionment of Human Diversity), then by the publication of the counter argument, known as Lewontin's fallacy.

Lewontin was a pioneer of the use of molecular biology in population genetics. The DNA sequencing era started approximately with the Maxam-Gilbert sequencing method in 1977, but in the days before, estimating the genetic diversity of a population was a challenging task. To do so, you needed visible markers that told you something about the genes of individuals, or more precisely that informed you about their alleles. Modern genetics was built on simple characters, such as the eye color in fruit fly, which have a Mendelian type of inheritance. But in natural populations, most of the traits are more complex and do not follow such simple rules. In that case, knowing the alleles of an individual is practically impossible (geneticists would say that they cannot infer the genotype from the phenotype).

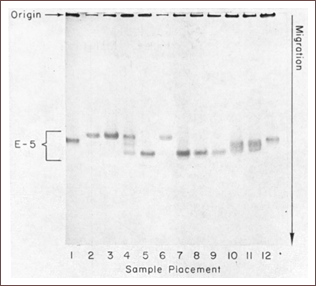This is where Lewontin and his colleague Jack Hubby had a genius idea. Instead of using hair or eye color, shapes of different appendices etc., they used characters that are invisible for the eye: molecules. They used electrophoresis, to separate the protein isoform coded by allele A from the isoform coded by allele a. The picture on the left, taken from A Molecular Approach to the Study of Genic Heterozygosity..., is one of the first experiments run by Lewontin and Hubby. By doing so, they suddenly gained access to a large spectrum of characters with simple Mendelian inheritance.

Using such molecular techniques, Lewontin set out to study the diversity of the human population, and found that for most such characters, racial groups accounted for 6.3% of the variability. In other words, the genetic difference between two people of different races is only 6.3% larger than between two people of the same race (click on the Penrose triangle below for a more detailed view of this computation).

As of today, nothing has been revised in this work, even though the estimates have varied somewhat between studies. The fallacy is in Lewontin's interpretation of his results. He concluded that it is impossible to distinguish a Caucasian from an African and therefore that races do not exist*.

In 2003, long after this statement made its way to the textbooks, the statistician and geneticist Anthony W. F. Edwards took on the difficult task of challenging this conclusion in an article entitled Human genetic diversity: Lewontin's fallacy. Even if it is impossible to distinguish a Caucasian from an African with a single gene, the distinction is quite easy to make with more genes. Just like in the guessing game, you may not guess what your partner is thinking of in a single question, but if you are allowed to ask many, you are near certain that you will guess right in the end. It seems that crimestop (see Lessons from Intelligent Design) took hold of Lewontin, as if he did not want to see the distinction, as if he did not want it to be possible.

One of Edwards' final remarks is that

it is a dangerous mistake to premise the moral equality of human beings on biological similarity because dissimilarity, once revealed, then becomes an argument for moral inequality.

Most of the time, genes tell apart a Caucasian from an African. Does that mean that they have different rights? Does that mean that one deserves more than the other? Does that mean that the life of one is worth more than the life of the other?

Erratum (February 2, 2013)

Johnathan Kaplan in the comments below pointed out a serious mistake, which I marked by a star in the text. Lewontin did not claim that it is impossible to distinguish a Caucasian from an African. Instead, he made the point that racial classifications ignore the bulk of human diversity and therefore bear no meaning for taxonomy.

The claim of A. W. F. Edwards is that this argument is invalid because we can build very accurate racial classifiers by taking several genes into account — and not a single gene at a time, as did Lewontin.

Needless to say, if someone fell prey to crimestop, it is rather me than Lewontin. It seems I genuinely wanted him to have made a logical mistake, and that it was the only way I could understand his argument, even when he clearly expressed a more elaborate point of view (see the discussion below for more detail).