With this post I inaugurate the focus on series, where I go much more in depth than usual. I could as well have called it the gory details, but focus on sounds more elegant. You might be in for a shock if you are more into easy reading, so the focus on is also here as a warning sign so that you can skip the post altogether if you are not interested in the detail. For those who are, this way please...

In my previous post I exposed the multiple testing problem. Every null hypothesis, true or false, has at least a 5% chance of being rejected (assuming you work at 95% confidence level). By testing the same hypothesis several times, you increase the chances that it will be rejected at least once, which introduces a bias because this one time is much more likely to be noticed, and then published. However, being aware of the illusion does not dissipate it. For this you need insight and statistical tools.

Fail-safe $(n)$ to measure publication bias

Suppose $(n)$ independent research teams test the same null hypothesis, which happens to be true — so not interesting. This means that the null hypothesis is tested $(n)$ times independently with an exact chance of 5% of being rejected. The probability that the $(n)$ teams accept the null is $(0.95^n)$. The complementary event, that at least one team will reject the null hypothesis and report the rejection is thus $(1 - 0.95^n)$. This number approaches 1 as $(n)$ goes large, so it becomes almost certain that the null will be rejected.

In the early days of meta-analysis, it was common to estimate the publication bias of a claim by computing what is known as a fail-safe $(n)$, i.e. the estimated number of unpublished studies that came to the opposite conclusion, given that the null hypothesis is true. If this number is credible given the research effort on the topic, the validation can be interpreted as an accident. If the fail-safe $(n)$ is large, this is evidence that the validation was not produced by over testing.

Let us illustrate this with an example. After meta-analysis, a claim has a fail-safe $(n)$ of 4. Should that claim be unjustified, we would need to imagine that it was the subject of 4 independent studies, one of which reported it by mistake. Quite possible for many fields of investigation. Another claim has a fail-safe $(n)$ of 8,768. If it were reported by mistake, we would need to imagine that as many groups of researchers worked on the same hypothesis. In most fields of research this would be considered too high, and it is more likely that the claim is correct.

The simplest way to compute a fail-safe $(n)$ is to consider that the number of reported publications has a binomial distribution with parameter $(p = 0.05)$ and $(n)$ unknown. The probability that $(k)$ studies are published is

$$ {n \choose k} \times 0.05^k \times 0.95^{n-k}, $$

where $(k)$ is observed. It is possible to choose the value of $(n)$ that maximizes the above probability to obtain the maximum likelihood estimate of $(n)$. For $(k = 1)$, this is 20, for $(k = 2)$ this is 40 and more generally, this is $(20k)$ (click on the Penrose triangle for a proof).

This approach is very coarse and has a heuristic purpose only. In practice, the computation of fail-safe $(n)$ is more complex, but I won't linger on it because the tool is no longer used. It has been replaced by more specialized methods to estimate the publication bias, because the estimates turned out to be unreliable.

The Šidák correction

So far I have assumed that there is only one hypothesis which is tested several times, but the multiple testing problem is more general. If a statistician tests 20 hypotheses, it is expected that s/he will validate one of them, even if those hypotheses are unrelated. For instance, the patients of a hospital could be diagnosed for 20 different mental disorders with a specificity of 95%. For each disorder, there is then a 5% chance that the patients are declared positive, even if they do not actually have the disease.

If we assume that the results of the 20 tests are statistically independent for sane patients, the probability that they are considered sane is $(0.95^{20} = .358)$. About 65% of sane people will be considered insane. This is not cool. Even though the null hypotheses are unrelated, rejecting any of them has the same consequence (the person will be declared insane). The tests are said to be part of a family, and the familywise error rate (FWER) in that case is 65%.

The gist of the Šidák correction is to find a replacement confidence level $(\alpha^*)$ for each test, such that the proportion of sane people declared insane would be 5%. Plugging the new level in the equation above, we get $((1-\alpha^*)^{20} = 0.95)$, which solves to $(\alpha^* = 1 - \sqrt[20]{0.95} = 0.0026)$. In other words, the tests for individual disorders must have a specificity of 99.74% so that the whole procedure has only a 5% chance of declaring a sane person insane.

The general formula of the Šidák correction is $(\alpha^* = 1 - \sqrt[n]{1-\alpha})$, where $(\alpha^*)$ is the replacement threshold for individual tests, $(\alpha)$ is the FWER, and $(n)$ is the number of tests performed. As regards multiple testing correction, it is customary to adjust the p-values instead of correcting the threshold. The Šidák-corrected p-value $(P)$ is thus $(P' = P\frac{\alpha}{\alpha^*})$, and a null hypothesis will be rejected if $(P' < \alpha)$ (we compare the adjusted p-values to the original threshold).

The Bonferroni correction

There are times when you cannot assume independence between the tests and thus cannot use the Šidák correction. For instance, it may be known that tests for depression and bipolar disorder in the previous example tend to report positive together. In that case you cannot use the Šidák correction.

The idea of the Bonferroni correction is to replace the threshold of each test by a value $(\alpha^*)$ such that the FWER is less than 0.05. In that case we cannot know the false positive rate, but we can control it by an acceptable bound.

If we call $(A_i)$ the event that the patient tests positive for disorder $(i)$, the aim is $(P(A_1 \cup \ldots \cup A_{20}) \leq 0.05)$. Note that if we set $(P(A_1) = \ldots = P(A_{20}) = \alpha^* = 0.05/20)$, we obtain

$$ \begin{eqnarray} P(A_1 \cup A_2 \cup \ldots \cup A_{20}) &=& P(A_1) + P(A_2 \cup \ldots \cup A_{20}) - P \left( A_1 \cap (A_2 \cup \ldots \cup A_{20}) \right) \\ &\leq& P(A_1) + P(A_2 \cup \ldots \cup A_{20}) \\ &\leq& P(A_1) + P(A_2) + P(A_3 \cup \ldots \cup A_{20}) \\ &\ldots& \\ &\leq& P(A_1) + P(A_2) + \ldots + P(A_{20}) = 20 \alpha^* = 0.05, \end{eqnarray}$$

where we have only used the axiomatic definition of probability and did not require independence, so the Bonferroni correction is more general than the Šidák correction. Consistenly, the Bonferroni-adjusted level $(\alpha^*)$ is smaller (0.00250 versus 0.00256). But not that much smaller. The object of the next technical section is to show that, for a low FWER, these methods are asymptotically equivalent. It is somewhat surprising that the hypothesis of independence does not make a substantial difference for FWER control.

This observation is perhaps the reason that the Šidák correction is sometimes mistakenly referred to as the Bonferroni correction. In any case, both corrections are considered to be too conservative by many statisticians. In other words, they do a good job when all the null hypotheses are true, but they perform poorly if one or more of the null hypotheses are false. To follow up on the previous example, setting the individual threshold from 5% to 0.25% makes it much less likely that a patient will be declared positive, even if s/he has the sickness.

Sorted p-values

Before going into the detail of the Benjamini-Hochberg correction let us tackle a question that will turn out to be useful. What is the distribution of the p-value if the null hypothesis is true? By definition the probability of obtaining a p-value lower than 0.05 is 0.05. Similarly, the probability of obtaining a p-value lower than 0.01 is 0.01, and by extension, for any number $(x)$ between 0 and 1, the probability of obtaining a p-value lower than $(x)$ is $(x)$. The property $(P(u \leq x) = x)$ defines the cumulative density of a uniform random variable $(U)$ in $((0,1))$. So under the null hypothesis, p-values are uniformly distributed. Performing $(n)$ independent statistical tests when all null hypotheses are true is the same as collecting an independent and uniform sample of size $(n)$. As a consequence, testing multiple null hypotheses can be reduced to testing whether a sample is drawn from a uniform distribution.

Plotting the sorted p-values is a very good way to see whether they follow a uniform distribution. If all the null hypotheses are true, the sorted p-values will lay on that straight line joining 0 to 1. If some of the null hypotheses are not true, the corresponding p-values will tend to be smaller, which will skew the plot near the origin. The following technical section shows the R script that I used to produce the figure below.

# Set up a reproducible random example.
set.seed(123)
# Initialize a vector of length 1000 to hold p-values.
p.values <- rep(NA, 1000)
# Perform 1000 one-sample t-tests on Gaussian samples (H0 is true).
for (i in 1:1000) {
   p.values[i] <- t.test(rnorm(100))$p.value
}
plot(sort(p.values), type='l', ylab="Sorted p-values")

set.seed(123)
p.values <- rep(NA, 1000)
# Perform 970 one-sample t-tests on Gaussian samples (H0 is true),
# and 30 tests on Gaussian samples with mean 0.35 (H0 is false).
for (i in 1:970) {
   p.values[i] <- t.test(rnorm(100))$p.value
}
for (i in 971:1000) {
   p.values[i] <- t.test(rnorm(100, mean=0.35))$p.value
}
plot(sort(p.values)[1:200], type='l', ylab="First 200 sorted p-values")
lines(30, .2, col=2, type='h')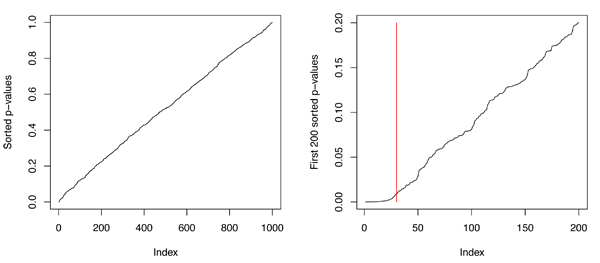

I plotted 1,000 sorted p-values when all 1,000 null hypotheses are true (left panel) and when 30 of them are false (right panel). The right plot is a zoom on the first 200 sorted p-values to emphasize the shape of the graph close to the origin. As you can appreciate, the left plot is a relatively straight line. The right plot also looks like a straight line, except that there is a flat region before the red line at index 30. This approach is very sensitive, as we can easily detect that ~ 3% of the hypotheses are false, but it is only qualitative. And this is where the Benjamini-Hochberg correction enters.

FDR and the Benjamini-Hochberg correction

The idea of the Benjamini-Hochberg correction is to give a different threshold to each of the sorted p-values. The series of thresholds is $(\left( \frac{0.05}{n}, \frac{2 \times 0.05}{n}, \frac{3 \times 0.05}{n}, \ldots \right))$, which lays on a straight line from the origin with a slope of $(0.05/n)$ as shown in the figure below where the data is the same as in the right panel above.

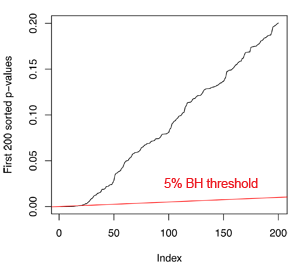
All the null hypotheses are accepted if the curve of the p-values is above the red line in a neighborhood of the origin. The FWER of that procedure is lower than 0.05 as we can easily show. The curve of the p-values is locally above the red line if and only if the lowest p-value is higher than $(0.05/n)$, or equivalently if all p-values are higher than $(0.05/n)$. This is the same criterion as the Bonferroni correction, which was shown to have a FWER lower than 0.05.

So what is the difference with Bonferroni correction then? In their seminal paper of 1995, Benjamini and Hochberg introduce the concept of false discovery rate (FDR). The typical scenario in a multiple testing situation is to reject a couple of null hypotheses and accept the others. FWER, as the probability of rejecting at least one null hypothesis when they are actually all true, does not distinguish between rejecting one hypothesis and rejecting them all. However these situations are very different. One may be right in rejecting one null hypothesis only, and wrong in rejecting them all, so we would like to have a way to tell which of the two is more accurate. The FDR is by definition the expected number of false discoveries, i.e the mistakes in the set of rejected hypotheses. Put simply, if the FDR of a set of rejected null hypotheses is 5%, it means that 5% of them are expected to be true (rejected by mistake).

The full Benjamini-Hochberg procedure is to reject all the hypotheses for which the p-value is below the red line (up until the first intersection if the lines cross several times), and accept the others. The main contribution of the authors was to prove that when tests are independent, the FDR of the rejected null hypotheses is lower than 5%. The proof of this theorm is not difficult, but it is too long and tedious to fit in this post.

Note that when using the Bonferroni threshold, the hypotheses rejected by applying the same procedure form a subset of the hypotheses rejected when using the Benjamini-Hochberg threshold. This is why the Bonferroni procedure is considered to be too conservative. It can be used to ensure that the FDR is lower than 5%, but the actual FDR might be well below that value. To follow up on the numerical example pictured above where 30 null hypotheses are false, the Bonferroni procedure rejects 5 hypotheses while the Bonferroni procedure rejects 17. The Bemjamini-Hochberg procedure does not reject all the false null hypotheses, it just finds a bigger set with less than 5% expected mistakes.

The rise and fall of multiple testing

In spite of all words of caution, correcting for multiple testing is sometimes considered metaphysical or optional. Even though I have the opposite opinion, that correcting for multiple testing is practical and mandatory, I admit that it is sometimes hard to know what correction to apply. The difficulty is not in choosing a procedure, or computing the thresholds, it is in understanding what you are actually doing.

As an example, suppose a professional statistician works for 100 different clients with a single null hypothesis each. After about a year s/he has tested all the null hypotheses. Should s/he apply FDR correction for performing 100 tests? Take a moment to think about it. Make yourself an opinion before you read on.

I believe the answer is no. If there were 100 statisticians performing one test each, they would (most probably) come to the same conclusions as a single statistician performing all the tests, but then we would not feel that there is any reason to apply a correction for multiple testing. When would you apply the correction then?

Suppose that all the clients of the statistician are start-up companies and that they all have the same null hypothesis, such that rejecting it means that they are doing better than their competitors. If the statistician is in for extra money s/he could buy stock from some of these companies. For that s/he has to choose a trusted subset expected to contain less than 5% false positives, which s/he could do by the Benjamini-Hochberg procedure.

The paradox is that the statistician will tell some companies that they are doing better than their competitors but s/he will not invest in those companies. The reason is that these are two different questions. If all of the clients are doing worse than their competitors, on average the statistician will tell 5 of them that they are doing good. This subset consists of 100% false positives. In short, knowing that you have a 5% error rate when the null hypothesis is true does not guarantee in any way that 5% of the null hypotheses you have rejected are actually true.

By construction, statistical testing procedures control the rate of false positives per test. If you want to control the rate of false positives per identified positive you should use FDR. This toy example illustrates one of the many pitfalls of multiple testing correction. There is much more to tell about the subject, but I feel I have already covered a lot of ground and every post, even a “focus on”, has to come to an end.